单人纸牌(Elevens Lab)活动3：洗牌

导言

回想一下你是怎么用手洗牌的。这种方法让扑克牌在牌组中顺序随机化的程度有多好？

探索

我们现在考虑洗牌，即将牌的顺序调换以得到看上去随机的序列。对于洗牌的要求是任一特定的顺序和其他的顺序有同样的出现几率。我们将使用Math.random method来生成随机数以决定这些顺序。

有不少洗牌的实现思路。我们考虑以下这两种：

完美洗牌

扑克牌玩家通常把牌分为两堆，然后将将一堆的牌插入到另一堆牌间。

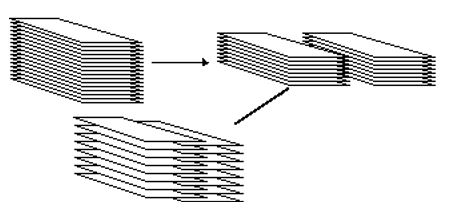
如果洗牌后相邻的两张牌分别来源于两堆，这个过程被称为完美洗牌。不幸的是，完美洗牌无法生成所有可能的顺序组合。事实上，对于52张的扑克牌组而言，八次完美洗牌会让牌组的顺序还原！

考虑以下这个完美洗牌算法，其接受cards数组作为输入，并将完成洗牌后的牌组以shuffled输出。

将shuffled初始化为52个空元素
设k为0
对于j在0与25之间
  将cards[j]复制为shuffled[k]
  设k为k+2
设k为1
对于j在26与51之间
  将cards[j]复制为shuffled[k]
  设k为k+2

这一方法把cards的前一半移动到shuffled的偶数位置，把cards的后一半移动到shuffled的奇数位置。

以上算法能够正确洗52张的牌组。如果需要洗奇数张牌组，shuffled数组的偶数索引则会比奇数索引多一个。因此，第一个循环需要比第二个循环多复制一张牌。这意味这在计算牌组中间索引时需要进一位。换言之，第一个循环中j要到(cards.length + 1) / 2 - 1，第二个循环则从之后开始。

选择洗牌

考虑以下算法，同样是接受cards数组作为输入，并将完成洗牌后的牌组以shuffled输出。我们将其命名为选择洗牌。

将shuffled初始化为52个空元素
对于k在0与51之间
  不断生成0与51之间的随机整数j，直到card[j]有一张牌
  将cards[j]复制为shuffled[k]
  将cards[j]设为空

这种方法为牌组中的k位置找到合适的牌，已经洗过的牌则不被考虑。

虽然这是一个相对完美洗牌而言更靠谱的方法，其最大的缺陷在于运行速度太慢。每当选到一个空元素时又需要重新生成新随机数。为决定shuffled的最后一个元素，平均要调用52次随机数生成器。

改进版的高效选择洗牌如下所示：

对于k在51与1之间
 生成0与k之间的随机整数r
 交换cards[k]与cards[r]

这受到了选择排序的启发：

对于k在51与1之间
 找到cards[0]与cards[k]之间最大值的位置r
 交换cards[k]与cards[r]

选择排序算法能够在一轮中找到用来进行交换的最大值或最小值，因而效率很高。

练习

1. 使用目录中的Shuffler.java文件来实现上一节中讨论的完美洗牌和高效选择洗牌。暂时先对整数数组进行操作。
2. Shuffler.java还提供一个调用洗牌method的main method。执行它并查看输出，确认每个洗牌方式把数组元素随机化的程度有多好。在执行过程中你应该换用不同的SHUFFLE_COUNT和VALUE_COUNT。

问题

1. 写一个名为flip的static method，模拟掷硬币的过程并在每次调用后返回heads或tails。得到heads的几率是tails的两倍，因而flip返回的heads次数在多次之后会是tails的两倍。
2. 写一个名为arePermutation的static method，就两个等长、无重复元素的int数组，当一个是另一个的一种不同排布时返回true，否则返回false。
3. 假定Shuffler.java中values数组的初始内容是{1, 2, 3, 4}。对于高效选择洗牌而言，需要怎样的随机数才会把values变成{4, 3, 2, 1}？