最近在上课时候，被我们学员问住了。执行这个看似简单的程序，猜猜看结果会是多少：

FloatError.java

public class FloatError {
  public static void main(String[] args) {
    System.out.println((3.0+4)/(1+4.0)*2-3);
  }
}

随便哪个高年级小学生都会告诉你答案是-0.2，但是实际Java算出来的结果会是-0.20000000000000018。这是什么鬼呢？

当然还有这个了
FloatError.java

public class FloatError {
    public static void main(String[] args) {
        System.out.println(Math.sin(Math.PI));
    }
}

随便哪个初中生都会告诉你答案是0，但是实际Java算出来的结果会是1.2246467991473532E-16。这又是什么鬼呢？

其实我对浮点数也不是太熟，因为从来没有认真学过这块，一开始想当然解释还解释错了两回。之后仔细做了一些研究，总算是搞明白了。

---

首先我做了一些简单的测试，看问题到底出在哪

FloatError.java

public class FloatError {
    public static void main(String[] args) {
        double a=(3.0+4)/(1+4.0)*2;
        System.out.println(a);
        System.out.println(a-3);
        System.out.println(a==2.8);
        System.out.println(2.8-3);
    }
}

结果是：

2.8
-0.20000000000000018
true
-0.20000000000000018

很意外，发现误差居然是减法带来的，难道Java就真的这么蠢，连2.8-3都算不对么？

---

要理解这个问题，我们需要温习一下科学记数法(scientific notation)。大家应该都知道，0.0000000056可以表示成\(5.6\times10^{-9}\)，当然150不怕麻烦的话也可以写成\(1.5\times10^{2}\)。很显然，计算机内部诸如double之类的浮点数也是采用类似的方式表示，这样一来我们就能够处理相当大范围内的数了。这里有一张英文PPT讲得很好：

显然，计算机内部是没有十进制的，所有的数字，即底数部分(base)和指数部分(exponent)，都要转换成二进制存储。我们试着按图索骥转换一下2.8。

\(\begin{split}2.8 & =1.4 \times 2^{1} \\
& =(1+0.25+0.125+\dotsb) \times 2^{1} \\
& =(1+0\times2^{-1}+1\times2^{-2}+1\times2^{-3}+0\times2^{-4}+\dotsb) \times 2^{1} \\
& =(1.0110\dots)_{2} \times 2^{1} \end{split} \tag{1}\)

当然我是懒得手算了，这边有一个网站可以随便算，反正小数部分结果是这个：

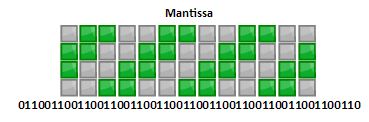
仔细看的话，会发现这是一个无限循环小数（repeating decimal，当然其实这边是二进制），因而是无法精确表示的。

当然还有一个小秘密就是计算机的中央处理器(central processing unit, CPU)内的浮点计算单元(floating-point unit, FPU)，又称为数学协处理器(math coprocessor)，在实际执行浮点运算(floating-point arithmetic)的时候，精度比double还要高……所以把double的2.8转换回十进制的话，就是2.79999999999999982236431605997，所以为啥是18而不是14或者16。结论是Java还是比你我要聪明一些的。

---

好吧，其实你并不需要知道以上这些就能做一个合格的程序员。但是作为程序员或者准程序员的话，你需要知道什么呢？

第一，我上面的测试部分其实给出了一个错误的示范。绝对不要用==来比较两个浮点数，请用>和<来限定范围，或者在某些情况下直接用(int)来强制cast成int。

第二，复杂的办法是采用java.math.BigDecimal，简单的办法是采用：

FloatError.java

public class FloatError {
    public static void main(String[] args) {
        System.out.println(String.format( "%.8f", Math.sin(Math.PI)));
    }
}

世界和平万岁！